Rectificación de la circunferencia.
Rectificar una circunferencia,
es llevar sobre una línea recta,
la magnitud de su arco.
Método de Arquímedes.
Se divide el diámetro A - B de la circunferencia
en siete partes iguales,
y, sobre la prolongación de éste,
se llevan quince más.
Conclusión: veintidos séptimas partes
del diámetro A - B,
equivalen a la rectificación
de la circunferencia, completa,
que es el segmento C - B.
Método de Specht.
A la circunferencia,
se le traza un diámetro AB.
Y en A, una perpendicular, P.
Después, se describe un arco
con centro en A,
y radio, el de la circunferencia,
obteniendo el punto C.
Dividimos un radio en cinco partes iguales,
y tres de ellas,
las llevamos a partir de C,
y una,
a continuación de B.
Unimos el centro de la circunferencia, 5,
con 3 de la perpendicular,
y por 1, (debajo de B),
trazamos una paralela a este segmento,
que nos corta a la perpendicular P,
en el punto D.
El segmento AD,
es la rectificación
de la circunferencia completa.
Método de Kochauski.
Se traza un diámetro AB
y en el punto B
una tangente T.
Desde el centro de la circunferencia O como vértice,
se dibuja un ángulo de 30º,
cuyo lado, al prolongarlo,
nos cortará a la tangente en C.
A partir de este punto,
se lleva la magnitud del radio tres veces.
La recta que une 3 con A,
es la rectificación
de MEDIA CIRCUNFERENCIA.
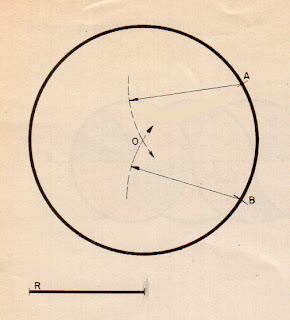
Método de Mascheroni.
Se traza un diámetro,
y con centro en sus extremos, A y B,
se describen dos arcos
de igual radio al de la circunferencia,
obteniendo los puntos 1 y 2.
Con centro otra vez en A y en B,
y radio A2 u B1,
vuelven a trazarse arcos,
que nos dan el punto 3.
Por último,
con centro en 2,
y radio la distancia hasta 3,
conseguimos el punto 4.
La recta que une 4 con B,
es la rectificación
de la CUARTA PARTE
de la circunferencia.
Procedimiento para rectificar
menos de un cuarto
de circunferencia.
Sea el arco AB,
el que queremos rectificar.
Trazamos un diámetro,
y, sobre su prolongación,
llevamos tres cuartas partes del radio.
En A,
se dibuja una perpendicular P,
unimos 3 con B,
y nos cortará a la perpendicular en C.
El segmento AC,
es la rectificación buscada.
(Archivo: cuevadelcoco).