Trazar una circunferencia
que pase por tres puntos
no situados en línea recta.
Los puntos son A, B y C.
Los unimos con dos segmentos de recta,
y a los dos segmentos les trazamos
las mediatrices,
que prolongamos
hasta que se corten
en el punto O.
El punto O es el centro de la circunferencia,
y el radio,
la distancia desde O,
a cualquiera de los tres puntos,
A, B y C.
Hallar el centro y el radio
de una circunferencia.
Se traza una cuerda cualquiera, A, B.
A ésta, se le traza su mediatriz,
y obtenemos el diámetro.
Al diámetro,
le trazamos otra mediatriz,
y obtenemos el centro, O.
Uniendo O con cualquier punto
de la circunferencia,
obtenemos el radio R.
Trazar una circunferencia
de radio determinado
que, a su vez,
pase por dos puntos dados.
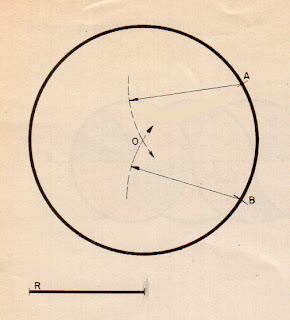
Sean los puntos A y B,
y el radio R.
Con el compás,
tomamos la magnitud de R,
y, haciendo centro en los dos puntos,
por los que queremos hacer pasar la circunferencia,
se trazan dos arcos.
Donde se cortan,
es el punto 0,
centro de la circunferencia.
División gráfica de la circunferencia.
Trazamos a una circunferencia,
el diámetro A, B.
Desde A,
tal como se aprecia en la figura,
trazamos una semirrecta,
y la dividimos
en tantas partes iguales
como queramos dividir a su vez
a dicha circunferencia.
Unimos el punto 1 con el extremo B del diámetro.
Trazamos paralelas a B-1,
y comprobamos
que hemos dividido el diámetro
en partes iguales.
Luego, haciendo centro en A y B,
dibujamos dos arcos,
que se cruzan en el punto C.
Uniendo C con la partición 2
del diámetro,
y prolongando
hasta cortar la circunferencia,
logramos el punto D.
El arco A-D,
es la séptima parte de la circunferencia,
en este caso.
Y si unimos los dos extremos
del arco A-D,
obtenemos el lado
del polígono regular inscrito.
Este procedimiento,
es universalmente válido,
y nos permite,
además de dividir la circunferencia
en N partes,
construir polígonos regulares
de N lados.
(Archivo: cuevadelcoco).



No hay comentarios:
Publicar un comentario