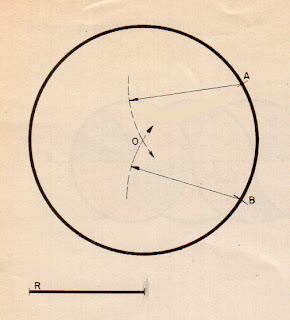
Dibujar un rectángulo,
dada su diagonal
y uno de sus lados.
Dibujamos la diagonal, D,
y hallamos su punto medio, O.
Con centro en éste,
y radio
la mitad de la diagonal,
describimos una circunferencia.
Después, y con centro
en los extremos de la diagonal, 1 y 2,
y con radio igual al lado dado,
obtenemos al cortar el arco de circunferencia
los puntos 3 y 4.
Vértices, junto con 1 y 2,
del rectángulo.
Dibujar un rectángulo,
dada su diagonal
y el ángulo que forma
con uno de sus lados.
Se dibuja la diagonal, D,
y sobre uno de sus extremos,
llevamos el ángulo dado, A.
Hallamos el centro de la diagonal
y, desde este punto, O,
describimos una circunferencia
que pase por los extremos de ella,
y que al cortar a un lado del ángulo,
nos dará el punto 2.
Unimos 2 con O,
y su prolongación nos da 3.
Éste punto, junto con el otro extremo de la diagonal, 4,
nos define el otro lado mayor.
Por último,
unimos 1 con 3,
y 2 con 4.
Dibujar un cuadrilátero cualquiera,
conociendo las magnitudes de sus cuatro lados,
y la de la diagonal.
Con centro en los extremos 1 y 2
del lado A,
describimos respectivamente, arcos de radio igual
a la diagonal D y al lado B,
obteniendo el punto 3.
Con centro en 3,
y radio C, trazamos otro arco,
que, con el que dibujemos con radio E
y centro en 1,
nos dará el punto 4.
Dibujar un trapecio isósceles
conocidas sus dos bases
y la altura.
Sobre una recta,
situamos la base mayor, B.
Hallamos su mediatriz,
y, sobre ella, llevamos la altura, A.
En este punto, trazamos una perpendicular,
y también con centro en A,
tomamos, a ambos lados,
la mitad de la otra base, B´.
Obtenemos los puntos 1 y 2,
que, unidos con los extremos de la base mayor,
nos dibujarán el trapecio buscado.
Dibujar un trapecio rectángulo,
dadas sus bases y su altura.
Se traza un ángulo recto,
y desde su vértice, V,
se toma sobre uno de sus lados
la magnitud de la base mayor B,
y, sobre el otro, la altura A,
obteniendo los puntos 1 y 2,
respectivamente.
Por 2, se traza una paralela a la base mayor, B,
y se lleva sobre ella la base menor B´.
Obtenemos así el punto 3,
que, unido con 1,
nos resuelve el problema.
Construir un trapecio escaleno,
conocidas sus bases.
Sobre una recta,
llevamos la magnitud de una base,
en este caso, la mayor, B.
A la distancia que queramos,
le trazamos una paralela,
sobre la cual, llevaremos
la magnitud del lado pequeño B´.
Uniendo sus extremos,
queda dibujado el trapecio,
siempre que tengamos en cuenta
que, para que sea escaleno,
sus lados tienen que ser desiguales,
y además, que ninguno de sus ángulos,
sea recto.
(Archivo: cuevadelcoco).